Mengenal Matriks: Pengertian, Jenis, dan Transpose

Pengertian Matriks

Matriks adalah sekumpulan bilangan yang disusun berdasarkan baris dan kolom, serta ditempatkan di dalam tanda kurung. Nah, tanda kurungnya ini bisa berupa kurung biasa “( )” atau kurung siku “[ ]”, ya. Suatu matriks diberi nama dengan huruf kapital, seperti A, B, C, dan seterusnya.

Misalnya nih, matriks di atas tadi, kita beri nama matriks A. Maka,

 

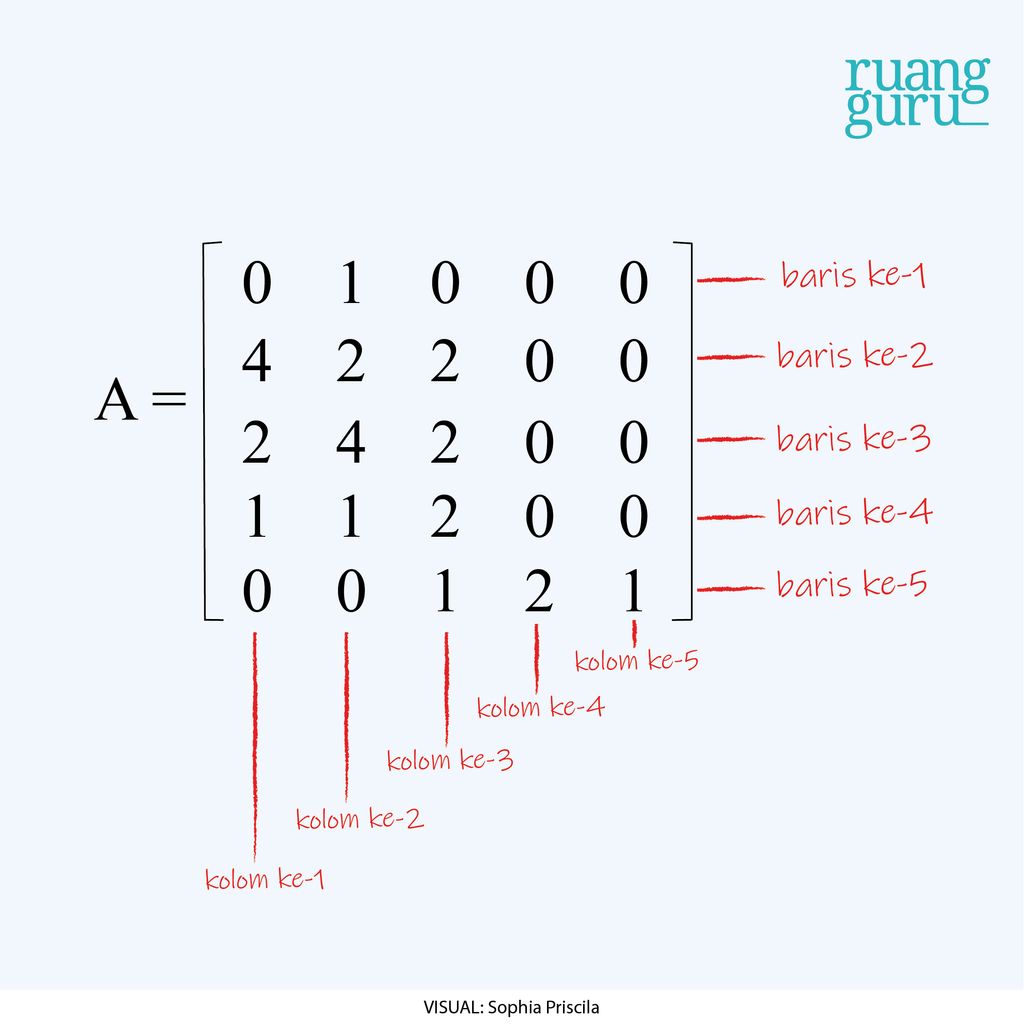
Penamaan baris dan kolom dibuat urut, ya. Jadi, baris ke-1 dimulai dari atas, urut ke bawah. Sementara itu, kolom ke-1 dimulai dari kiri ke kanan

Ordo dan Elemen Matriks

Matriks itu punya ukuran, guys. Ukuran matriks disebut ordo. Ordo matriks ini berdasarkan dari banyaknya baris dikali banyaknya kolom pada matriks. Jadi, kalo suatu matriks A memiliki m baris dan n kolom, maka matriks A tersebut berukuran (berordo) m x n. Supaya lebih sederhana, kita bisa menulisnya dengan Amxn.

Nah, masing-masing bilangan yang terdapat di dalam matriks disebut elemen matriks. Elemen-elemen matriks juga ada notasinya sendiri, lho. Kalo matriks dinotasikan dengan huruf kapital, maka elemen-elemen matriks dinotasikan dengan huruf kecil dan diberi indeks yang menyatakan letak baris dan kolomnya.

Misalnya nih, pada matriks A di atas, jumlah barisnya kan ada 5 dan jumlah kolomnya juga ada 5, maka ordonya adalah 5 x 5, atau bisa kita tulis A5×5. Lalu, untuk elemen-elemen matriks A bisa dinotasikan dengan aij, yang menyatakan elemen matriks A pada baris ke-i dan kolom ke-j.

Supaya kamu nggak bingung, langsung simak contoh di bawah ini aja, yuk!

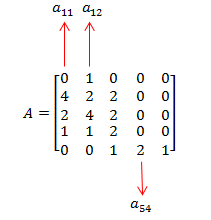
Kita ambil contoh a11, a12, dan a54, seperti pada gambar.

• a11 menyatakan elemen matriks A pada baris ke-1 kolom ke-1, nilainya adalah 0.
• a12 menyatakan elemen matriks A pada baris ke-1 kolom ke-2, nilainya adalah 1.
• a54 menyatakan elemen matriks A pada baris ke-5 kolom ke-4, nilainya adalah 2.

Gimana, paham kan cara bacanya?

Jenis-jenis Matriks

Selain punya ukuran (ordo), matriks juga terbagi menjadi beberapa bentuk yang mempunyai sifat khusus. Nah, beberapa jenis matriks khusus yang perlu kamu ketahui di antaranya sebagai berikut:

 

a. Matriks Baris

Matriks baris adalah suatu matriks yang terdiri dari satu baris aja. Contohnya,

 

Kalo kita lihat, matriks A, matriks P, dan matriks Q, semuanya terdiri dari satu baris dan beberapa kolom. Untuk masing-masing ordonya, berarti A1×3, P1×4, dan Q1×5.

 

b. Matriks Kolom

Kebalikannya dari matriks baris, matriks kolom adalah suatu matriks yang terdiri dari satu kolom aja. Contohnya,

 

Matriks R, matriks S, dan matriks T sama-sama terdiri dari satu kolom dan beberapa baris. Oleh karena itu, ordo matriksnya adalah R2×1, S3×1, dan T4×1.

 

c. Matriks Persegi

Matriks persegi adalah suatu matriks yang memiliki jumlah baris dan kolom sama. Itu tandanya, m = n. Karena jumlah baris dan kolomnya sama, maka ordo matriksnya bisa kita tulis menjadi n x n, atau matriks ordo n.

Pada matriks persegi, terdapat diagonal utama, yaitu elemen-elemen matriks yang letak barisnya sama dengan letak kolomnya. Selain diagonal utama, ada juga diagonal samping atau diagonal kedua. Kalo kita tarik garis di sepanjang diagonal utama matriks, maka diagonal samping ini berada di arah sebaliknya.

 

Nah, berdasarkan contoh di atas, matriks A memiliki jumlah baris dan kolom yang sama karena matriks ini merupakan matriks persegi, yaitu sebanyak 2. Maka, matriks ini merupakan matriks berordo 2. Kemudian, elemen-elemen pada diagonal utamanya adalah 8 dan 7. Coba deh, kalo matriks B, ordo dan diagonal utamanya apa aja, nih? Jawab di kolom komentar, ya!

 

d. Matriks Diagonal

Matriks diagonal adalah matriks persegi yang elemen-elemen selain diagonal utamanya bernilai nol. Contohnya,

 

Kalo kita perhatikan gambar di atas, elemen-elemen pada diagonal utama matriks Q adalah 3, 8, dan 5. Nah, di luar diagonal utama, semua elemennya bernilai 0. Misalnya, elemen Q12 adalah 0, lalu elemen Q21 juga 0.

 

e. Matriks Identitas

Matriks identitas adalah matriks persegi yang semua elemen pada diagonal utamanya bernilai satu, sedangkan elemen lainnya bernilai nol. Umumnya, matriks identitas dinotasikan dengan I disertai dengan ordonya. Contohnya,

 

f. Matriks Nol

Sesuai namanya, matriks nol adalah matriks yang semua elemennya bernilai nol. Matriks nol biasanya dinotasikan dengan huruf O disertai ordonya. Contohnya,

 

Transpose Matriks

Transpose matriks adalah suatu matriks yang diperoleh dari hasil pertukaran antara elemen baris dan kolomnya. Jadi, elemen-elemen pada baris akan kita tukar menjadi elemen-elemen pada kolom, atau sebaliknya. Pasti kamu bingung, kan?

 Misalnya, kita akan mentranspose matriks A dan B. Maka, matriks transposenya bisa dinotasikan dengan At dan Bt.

 

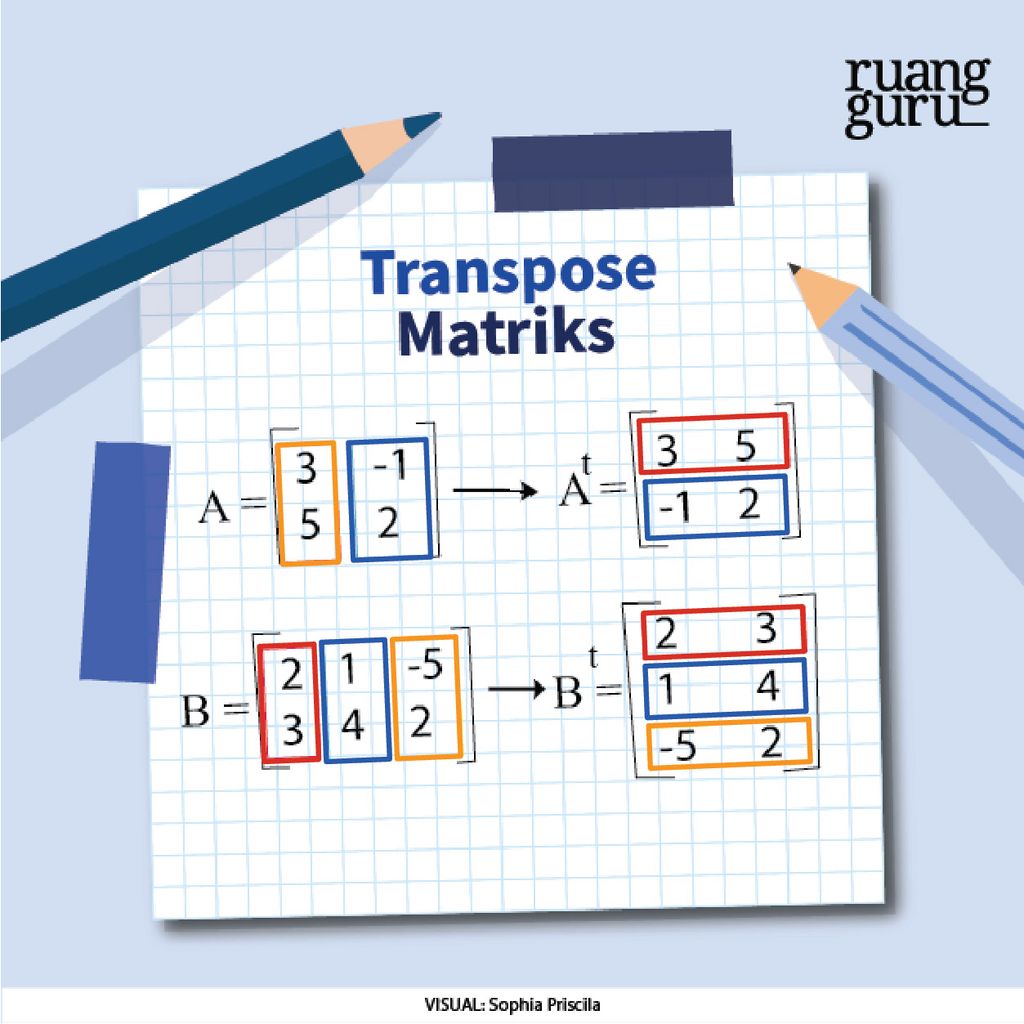
Nah, kalo kamu perhatikan kotak warna-warni pada matriks di atas, kamu pasti paham nih dengan polanya. Aku kasih contoh, ya. Coba kamu lihat matriks A dan At! Elemen-elemen baris ke-1 matriks At (yang di kotak merah), itu merupakan pertukaran dari elemen-elemen kolom ke-1 matriks A. Begitu juga dengan elemen-elemen baris ke-2 matriks At (yang di kotak biru), merupakan pertukaran dari elemen-elemen kolom ke-2 matriks A. Paham, ya?

Sekarang, coba kamu kerjakan contoh soal di bawah ini. Caranya sama kok kayak yang udah dijelasin sebelumnya.