Materi Notasi Sigma
Pengertian Notasi Sigma
Pembahasan pertama adalah pengertian dari sigma. Sigma biasanya disimbolkan dengan bentuk Σ yang menandakan penjumlahan suatu barisan bilangan.
Bentuk Umum dari Notasi Sigma
Setelah kamu belajar tentang pengertian sigma, pembahasan selanjutnya adalah bentuk umumnya. Jika kamu memiliki 199 suku bilangan dan ingin menjumlahkannya, maka kamu akan menuliskannya menjadi seperti di bawah ini.
U1 + U2 + U3 + …. + U199
Untuk memudahkan penulisan penjumlahan tersebut, kamu bisa menggunakan bentuk umum dari Sigma seperti di bawah ini.
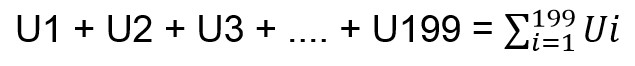
Sehingga bentuk umum dari notasi ini adalah sebagai berikut.
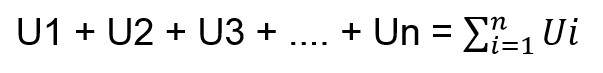
Sifat-sifat Pada Notasi Sigma
Selain bentuk umum di atas, Notasi ini juga memiliki beberapa sifat yang bisa digunakan untuk menyelesaikan soal-soal yang cukup rumit. Kamu bisa menggunakan sifat-sifat sigma di bawah ini dalam menyelesaikan soal sigma.

Contoh Soal dan Pembahasan
1. Diberikan bentuk dari sebuah pernyataan 
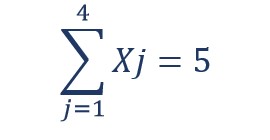
Tentukan hasil
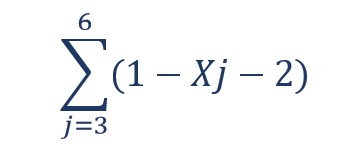
Untuk mengerjakan soal di atas, kamu bisa menggunakan salah sifat dari sigma. Kamu bisa memecah soal tersebut menjadi dua bagian seperti di bawah ini.
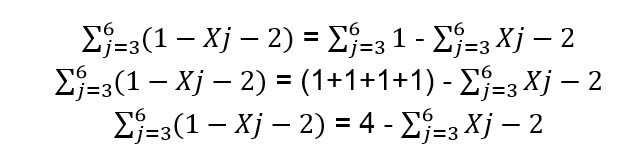
Dikarenakan bentuk
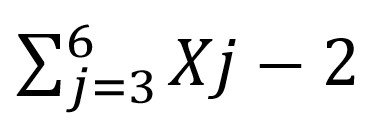
berbeda dengan bentuk pernyataan
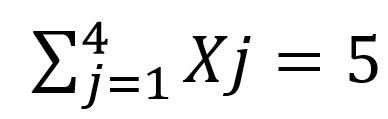
Maka kamu harus mengubah bentuk

dengan cara menghilangkan konstanta -2 seperti di bawah ini.
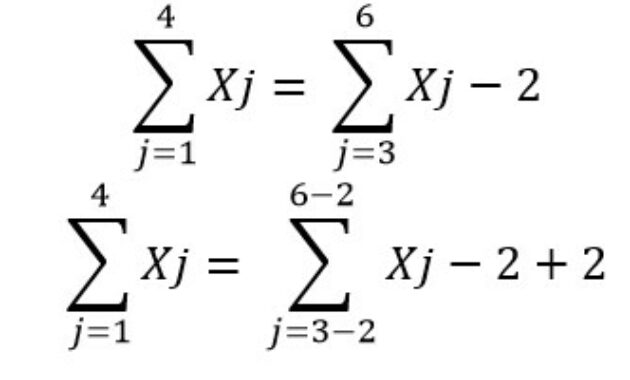
Sehingga penyelesaian akhirnya akan seperti di bawah ini.
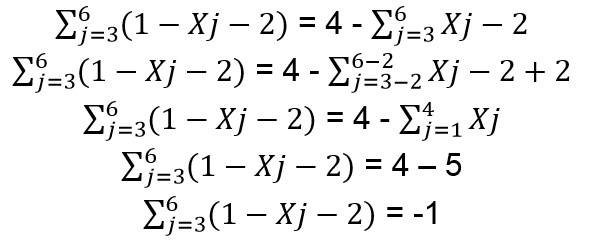
2. Diberikan sebuah pernyataan 
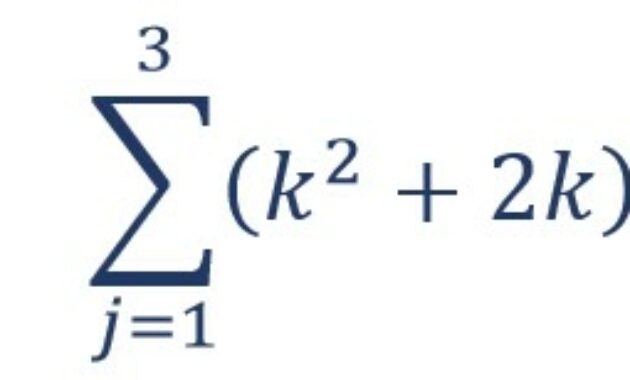
Berapakah hasil dari pernyataan tersebut
Untuk mengerjakan soal di atas, kamu bisa memecah soal tersebut menjadi bentuk yang lebih sederhana menggunakan sifat operasi sigma.
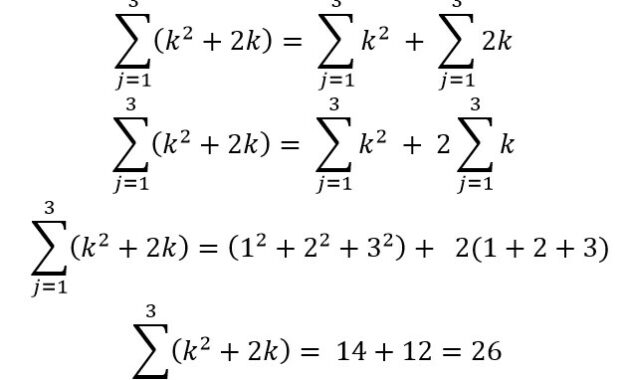
3. Diberikan sebuah bentuk
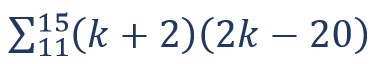
Tentukan hasil dari bentuk operasi sigma tersebut
Untu mengerjakan soal di atas, maka kamu harus menggunakan cara manual karena lebih cepat jika dibandingkan dengan penyederhanaan.
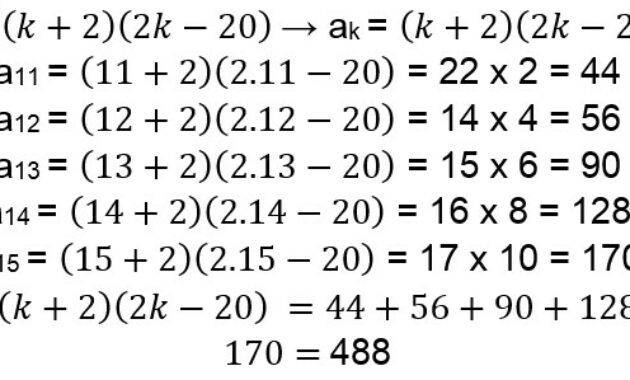
4. Diberikan sebuah deret 1 – 5 + 9 – 13 + 17 – …… + 130 – 133. Tentukan bentuk sigma dari deret tersebut
Untuk mengerjakan soal di atas, kamu harus memperhatikan deret di atas. Deret di atas memiliki pertama = 1 dan memiliki beda = 4.
Namun setiap suku genap memiliki nilai minus. Langkah awal yang perlu dilakukan adalah mencari jumlah banyak suku dalam deret tersebut menggunakan rumus deret aritmatika.
Un = a + (n-1)b
133 = 1 + (n-1)4
133 – 1 = (n-1)4
132 = 4n – 4
4n = 132 + 4
N = 34
Jumlah suku dalam deret tersebut adalah 34. Langkah selanjutnya adalah mencari bentuk suku ke-n pada deret tersebut.
Un = a + (n-1)b
Un = 1 + (n-1)4
Un = 1 + 4n – 4
Un = 4n -3
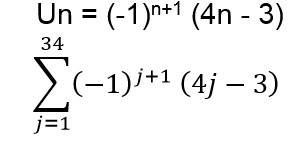
5. Diberikan sebuah deret -4 – 2 + 0 + 2 + 4 + 6 + …… + 26.
Tentukan bentuk sigma dari deret tersebut
Pertama yang perlu kamu lakukan adalah memperhatikan suku awal dan beda dari deret tersebut. Deret tersebut memiliki suku awal = -4 dan memiliki beda = 2. Sehingga kamu bisa mencari banyak suku pada deret tersebut.
Un = a + (n-1)b
26 = -4 + (n-1)2
26 = -4 + 2n – 2
26 = 2n – 6
2n = 32
N = 16
Setelah kamu mengetahui jumlah suku dalam deret tersebut, maka kamu bisa mencari rumus suku ke-n dari deret tersebut.
Un = a + (n-1)b
Un = -4 + (n-1)2
Un = -4 + 2n – 2
Un = 2n – 6
Kamu bisa mengubah bentuk dari rumus suku ke-n menjadi bentuk sigma dari deret tersebut seperti di bawah ini.
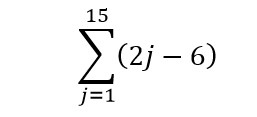
6. Diberikan sebuah notasi dengan bentuk
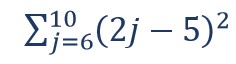
Tentukan bentuk sigma yang ekuivalen dengan bentuk tersebut.
Untuk mengerjakan soal di atas, kamu bisa menggunakan salah satu sifat bentuk sigma seperti di bawah ini.
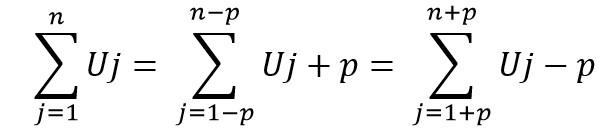
Sehingga bentuk soal di atas bisa di ubah mengikuti aturan sifat sigma.
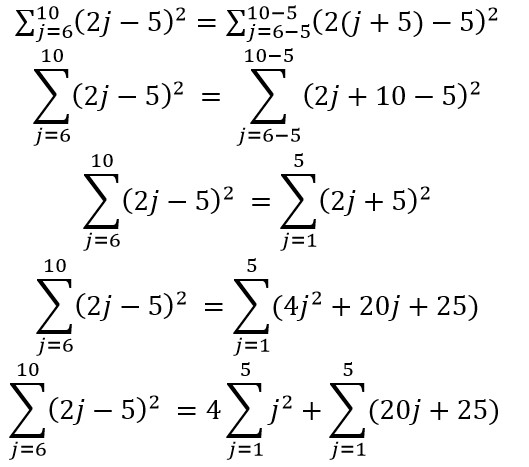
Jadi bentuk sigma yang ekuivalen dengan bentuk adalah
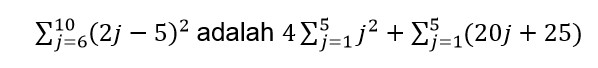
7. Jika diberikan sebuah bentuk

Untuk mengerjakan soal di atas, kamu bisa menyederhanakan soal tersebut menjadi seperti di bawah ini.
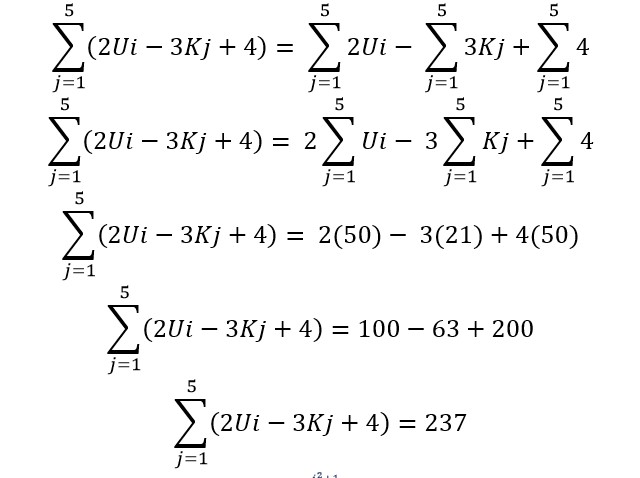
8. Diberikan sebuah bentuk sigma
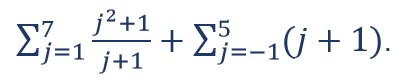
Buatlah bentuk sigma tersebut menjadi lebih sederhana
Kamu bisa menggunakan sifat operasi sigma seperti di bawah ini untuk mengerjakan soal di atas.
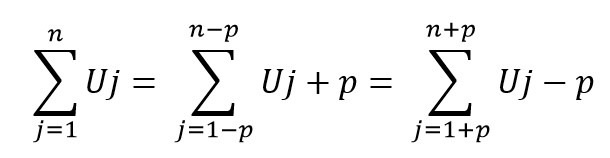
Kamu bisa menambahkan angka dua, sehingga proses pengerjaannya menjadi seperti di bawah ini
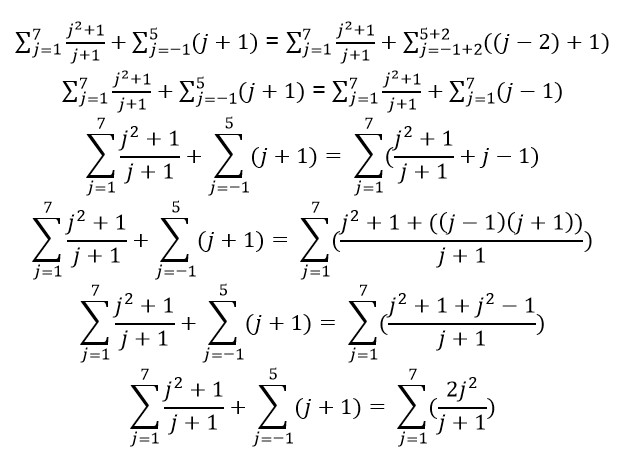
Maka:
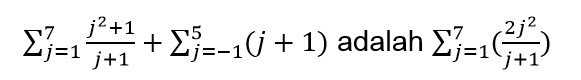




Tidak ada komentar:
Posting Komentar